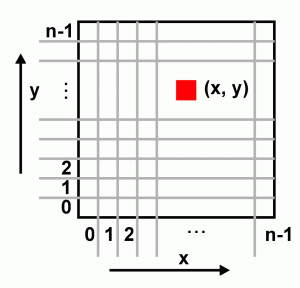
Koordinatenwerte werden modulo n betrachtet; dies stellt die zyklische Geschlossenheit sicher:
- (x + n, y) º (x, y)
- (x, y + n) º (x, y)
Genug getändelt. Endlich muß die Mathematik ein wenig zu ihrem Recht kommen.
Die Ausarbeitung dieses Textes stützt sich insbesondere auf Rouse Ball Mathematical Recreations and Essays, S. 193-208 und Martin Gardner Penrose Tiles to Trapdoor Ciphers, S. 293-306.
Ein allgemeines Konstruktionsverfahren für ungerade magische Quadrate kann aus dem Verfahren von LaLoubère hergeleitet werden. Wir betrachten ein Verfahren, das auf der Durchführung von zwei Elementarschritten und einer Zusatzbedingung aufbaut.
 |
Sei n = 2k+1 die Kantenlänge des magischen Quadrates. Die Zellen
des Quadratschemas werden nach Spalten und Zeilen indiziert; man verwendet
also eine ganz gewöhnliche Koordinatenbeschreibung der Position eines
Eintrages.
Koordinatenwerte werden modulo n betrachtet; dies stellt die zyklische Geschlossenheit sicher:
|
Ausgehend von einer im Zuge des Verfahrens belegten Zelle (x, y) wird die Folgezelle durch einen "Vektor" gegeben. Das Verfahren von La Loubère entspricht diesen Schritten:
Nach jeweils n Einträgen ist ein Schritt II nötig
Nach n-1 Schritten vom Typ II ist das Quadrat vollständig.
Eine Verallgemeinerung kann offenbar leicht angegeben werden:
Diese Verallgemeinerung erlaubt einige Folgerungen:
| Definition | Eine Schreibweise zu Kennzeichnung von magischen Quadraten nach dieser
Konstruktionsmethode ist:
|
|||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|||||||||||||||||||||||||||||||||
| Bemerkung | Die elementaren Konstruktionsmethoden sind gemäß dieser
Schreibweise:
|
|||||||||||||||||||||||||||||||||
Zwei Beispiele sollen die Anwendung des Verfahrens verdeutlichen.
Beispiel 1
|
Beispiel 2
|
Durch die Definition ergeben sich, was den strukturellen Aufbau der magischen Quadrate betrifft, starke Beschränkungen. Für die Kantenlängen 3 und 4 lassen sich einfache Formeln angeben, die die Bedingungen alle möglichen magischen Quadrate angeben. Beachte die Symmetrie in den Formeln bzgl. der Summanden und ihren Vorzeichen!
Bei Kraitchik, Mathematical Recreations, S. xxx fand ich folgendes einfache Schema für magische Quadrate der Kantenlänge 3. Martin Gardner zitiert diese Schema ebenfalls in Penrose Tiles to Trapdoor Ciphers
| a - c | a - b + c | a + b |
| a + b + c | a | a - b - c |
| a - b | a + b - c | a + c |
Für die Werte a,b,c,d gelten folgende einschränkende Bedingungen:
Ähnlich wie beim Lo Shu sollte man jedoch dieses Ergebnis ncht ungeprüft hinnehmen, sondern hinterfragen, warum genau dieses Schema alle magischen Quadrate der Kantenlänge 3 beschreibt. Eine systematische Herleitung kann sich dieselben Argumente zunutze machen, die von vorhin bekannt sind.
E. Bergholt gab 1910 dieses allgemeine Schema für magische Quadrate der Kantenlänge 4 an:
| A - a | C + a + c | B + b - c | D - b |
| D + a - d | B | C | A - a + d |
| C - b + d | A | D | B + b - d |
| B + b | D - a - c | A - b + c | C + a |
Veranschaulichen wir uns an der ersten Zeile, wie die magische Summe zustandekommt:
| (A-a) + (C+a+c) + (B+b-c) + (D-b) = A+B+C+D |
Die Summe der Felder im Mittelkarree ist folglich magisch. Ein Blick auf die Eckfelder zeigt uns:
| (A-a) + (D-b) + (B+b) + (C+a) = A+B+C+D |
Auch die Summe der Eckfelder ist magisch. Das ist zwangsweise bei jeden magischen Quadrat der Kantenlänge 4 der Fall.
Magische Quadrate der Kantenlänge 4 sind pandiagonal, wenn gilt:
| a = b = d - c = 1/2 (A - B - C +D) |
Sie sind symmetrisch, wenn die Bedingung erfüllt ist:
| a + c = d = b - c und A + C = B + D |
Die beiden Bedingungen schließen sich gegenseitig aus; ein magisches Quadrat der Kantenlänge 4 kann nicht gleichzeitig symmetrisch und pandiagonal sein.
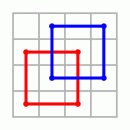
Eckfelder und Mittenfelder sind nicht die einzigen regelmäßigen Anordnungen, die in einem magischen Quadrat der Kantenlänge 4 aufscheinen. Man vergegenwärtigt sich leicht, daß auch zwei andere Anordnungen die magische Konstante ergeben. Die Kontrollrechnung erfolgt nach dem obigen Schema.
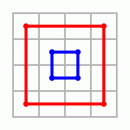 |
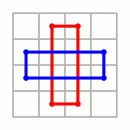 |
Abhängig von den Werten A,B,C und D ergeben sich zusätzliche Eigenschaften des Quadrates:
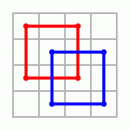
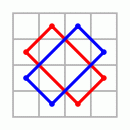
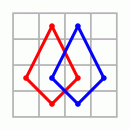
Wie weit das gehen kann, zeigt das Beispiel des "Dürer"-Quadrates aus dem Holzschnitt Melencolia. Die magische Summe m=34 läßt sich in einer überraschenden Anzahl zusätzlicher Anordnungen herauslesen
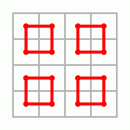 |
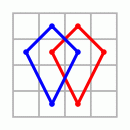 |
 |
||||||||||||||||
 |
 |
 |
Formeln dieser Art für Quadrate der Kantenlänge 5 und größer sind mir nicht bekannt. Die Vermutung liegt nahe, daß diese Formeln sehr schnell unübersichtlich werden.
Wir haben bereits erfahren, daß es ein einziges magisches Quadrat der Kantenlänge 3 gibt. Die vorhin gezeigten formalen Methoden lassen nicht nur die Frage aufkommen, ob damit alle magischen Quadrate einer bestimmten Kantenlänge erzeugt werden können, sondern auch wieviele grundsätzlich verschiedene magische Quadrate einer bestimmten Kantenlänge existieren. Die Fragen sind legitim, aber nicht gerade leicht zu beantworten. Bereits für die Kantenlänge 4 war das ein langwieriges Unterfangen. Heute sind diese Fakten bekannt:
So einfach die Fragestellung anmutet, so schnell scheitert der Versuch, eine geschlossene Formel für die Anzahl der möglichen Lösungen angeben zu wollen. Die exhaustive Methode, sprich das "Ausprobieren" aller möglichen Fälle scheitert an der Größe der Aufgabe, eine geeignete Buchführung über die gültigen Lösungen durchzuführen und an der kombinatorischen Explosion der möglichen Anordnungen in Abhängigkeit von der Ordnung n. Eine Obergrenze der Anzahl gibt die Tatsache, daß Symmetrie und Drehung ein Achtel aller technisch ausführbaren Anordnungen auswählen. Kombinatorisch ergibt sich damit die Obergrenze zu ((n2)!)/8, was zwar alle nicht-magischen Quadrate mit einschließt, aber doch einen Eindruck von den Dimensionen gibt, in die man sich vorwagt. Für n=6 gibt es damit
(36!)/8 = 46499165848737652183499931018854400000000 » 4,65 ·1040
grundsätzlich verschiedene Anordnungen der ersten 36 natürlichen Zahlen in einem quadratischen 6 ´ 6-Schema. Vergleicht man diesen Wert mit dem begründet geschätzten von 1,775399 ·1019 (lt. Trump), dann merkt man schnell, daß hier die "brute-force"-Methode, die magischen Quadrate daraus auszusieben, jämmerlich versagt. Die oben beschriebenen formalen Methoden liefern zwar beachtliche Teilmengen der möglichen Quadrate, jedoch bei weitem nicht alle Lösungen. Die sogenannten "wilden Quadrate", sowie die Rahmenquadrate werden davon nicht oder nicht vollständig erfaßt.
| zu den Programmcodes |
| Stand: 28.11.2006 / |
|